Tekrar merhaba arkadaşlar C++ ile ilgili olan yazılarımıza biraz ara verip bugün gerek oyunlarda, gerek coğrafi bilgi sistemlerinde, gerekse arazi görselleştirmesi, resim işleme ve bunun gibi bir çok alanda kullanılan bir veri yapısından kısaca bahsetmek istiyorum: “Quadtree“. Bu veri yapısının detaylarına çok girmeden önce “Spatial Data Structrues” ve “Spatial Partitioning” denilen yani Uzaysal Veri Yapıları ve Uzaysal Bölümleme konusunu bir bakalım.
Giriş
Bu tarz veri yapılarının en önemli amacı gerek görselleştirme gerek fizik işlemleri gerekse arama gibi işlerde yapılan karşılaştırma miktarını düşürmektedir (Bu sözü unutmayın nasıl sorusu bir sonraki başlıkta). Genel olarak hiyerarşik bir doğaya sahiptirler. Verinin yapısına dağılımına ve kullanım alanına göre kullanılacak veri yapısı belirlenir. Örneğin 2B noktasal veriler için “Grid” veya “Quadtree” daha öncelikli tercih edilmesi gerekirken 3 İç ortamlar için “BSP Tree” veri yapısı örneğin Octree’ye göre daha öncelikle tercih edilmelidir.
Aşağıda örnek bir Octree görebilirsiniz:

Aşağıda örnek bir BSP Tree görebilirsiniz:


Quadtree
Şimdi gelelim yazımızın solistine yani Quadtree’ye. Quadtree’ler temel olarak 2B uzayın eşit bir şekilde 4 e bölünmesine dayanır. Yani her bir ağaç düğümü (node) 4 çocuk düğüm içerir ve genel olarak ilgilenilen veriler en alt seviyedeki (“leaf”) düğümlerinde tutulur. Bölümleme genel olarak her bir düğüm için tutulacak olan nesne adeti aşıldığında gerçekleşir ve bu durumda ağaç düğümü bir kez daha bölünür ve nesnelere bu düğümlere dağıtılır. Genel olarak eklenen nesneler karesel olarak ilgili düğümlerin sınırları ile karşılaştırılarak dağıtılırlar. Aşağıdaki figür veri yapısını kafanızda canlandırmanıza yardımcı olacaktır. Her seviye bir önceki ile aynı sınırlara sahip olsa da, elemanların dağıtılabileceği düğüm sayısı alt seviyelere indikçe artmaktadır. Genel olarak bu derinlik sabit bir sayı olarak belirlenir.
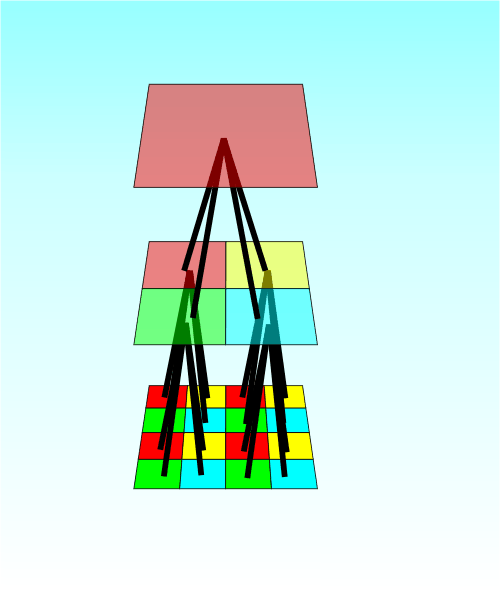
Yukarıdaki figürden de anlaşılacağı üzere aslında Quadtree’ler 4 çocuklu bir ağaç olarak ta düşünülebilirler. Aşağıda bu minvaldeki figürü görebilirsiniz.
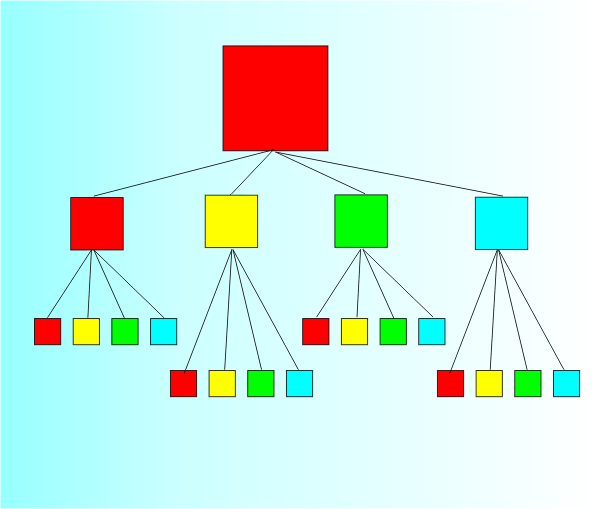
Wikipedia dan öğrendiğimiz kadarı ile bu veri yapısı ilk defa 197 yılında Raphael Finkel ve J. L. Bentley tarafından Q-Tree olarak adlandırılmıştır.
Aslında bu anlamda yukarıda bahsettiğimiz gibi “Binary Tree”‘ye oldukça benzemektedir, sadece iki çocuk yerine dört çocuğa sahiptir. Bir çok farklı varyasonu vardır (yazımın sonunda bir kaçına değineceğim), quadtree’ler içerdikleri veri tiplerine göre (nokta, çizgi veya poligon) sınıflandırılabilmektedirler. 3B uzayı düzgün bir şekilde bölmek için ise Octree veri yapısı kullanılmaktadır. Bu veri yapısı da uzayı eşit 8 parçaya bölmekte ve ağrılıklı olarak 3B nesneler için kullanılmaktadır. Bir de daha genelleştirilmiş olan kd-tree’ler vardır ki. Buna da ayrı bir yazı ayırmayı planlıyorum.
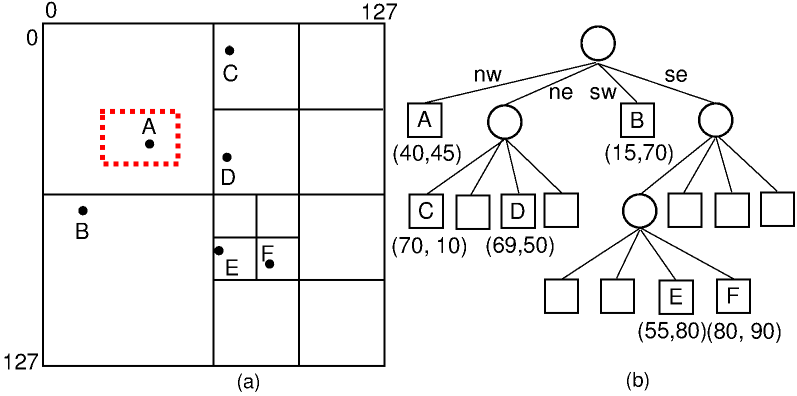
Şimdi gelelim yazımızın başında bahsettiğim “yapılan karşılaştırma miktarını düşürmektedir” ifadesinin Quadtree’ler için nasıl işlediğine. Bunu basit bir örnek üzerinden açıklamaya çalışacağım:
Şimdi yukarıda verildiği gibi 6 adet nesnemizin olduğu 2 boyutlu bir dünya düşünelim. Amacımız ekranımıza giren nesneleri görüntülemek. Mevcut ekranımızda kırmızı noktalı dikdörtgen ile gösterilsin.
Şimdi Quadtree kullanmadığımız durumda hangi noktaların gösterilmesi gerektiğini anlamak için bütün noktalar ile bu ekranın kapsadığını alanı karşılaştırmamız gerekiyor. Bu da 6 karşılaştırma demek. Quadtree kullandığımız durumda ise mevcut ekranımız quadtree’nin sol üst düğümü ile kesiştiği için sadece bu düğüme bakmamız yeterli ve bu durumda da sadece 1 karşılaştırma yetiyor. Ortalama şartlara baktığımızda quadtree ve genel olarak bu tarz uzay bölümleme veri yapıları bu noktada büyük avantaj sağlamakta.
Quadtree Operasyonları
Ekleme (“Insertion”)
- Eklenecek olan nesneyi içerecek (yani karesel alanı, quadtree düğümü sınırları içerisinde kalacak) dip (“Leaf”) düğümü bulunana kadar “recursive” olarak ilerlenir,
- Daha sonra ilgili düğüme nesne eklenir,
- Eğer nesnenin eklendiği düğümdeki nesne adeti izin verilen sınırlar içerisinde ise işlem tamamlanır,
- Eğer nesnenin eklendiği düğümdeki nesne adeti izin verilen sınırı aşar ise ilgili düğüm tekrar dörde bölünür ve nesneler bu düğümlere dağıtılır.
Silme (“Delete”)
- Silinecek olan nesneyi içerecek dip (“Leaf”) düğümü bulunana kadar “recursive” olarak ilerlenir,
- Daha sonra ilgili düğümden nesne silinir.
Sorgulama (“Query”)
- Kök düğümden başlanarak ilgili nesne ile düğümün sınırları karşılaştırılır ve kesişen düğüme kadar “recursive” olarak ilerlenir.
- Eğer kesişen bir düğüm bulunur ise o düğümdeki bütün nesneler karşılaştırılır.
- Benzer şekilde verilen dörtgensel bir alan ile kesişen elemanlar da bu şekilde bulunabilir.
Örnek Quadtree
Şimdi gelelim temel bir Quadtree sınıfına. Her veri yapısında olduğu gibi bu veri yapısı da özel
ihtiyaçlar doğrultusundan özelleştirilebilir ve de özelleştirilmelidir. Fakat ilk iterasyonda sizlere temel bir çok uygulama için ihtiyacınız karşılayacak ve genel quadtree mantığını anlatacak bir örnek vereceğim. Bu örneği baz alarak kendi ihtiyaçlarınız doğrultusunda bu veri yapısını güncelleyebilirsiniz.
- Örnek uygulamada görselleştirme için SFML kullandım. SFML ile ilgili kütüphanelerini https://github.com/yazilimperver/ProjectTemplates/tree/master/Ext adresinden alıp .sln dizinine yine Ext olarak kopyalayabilirsiniz,
- Visual Studio projesi için ise https://github.com/yazilimperver/DataStructures “repository” sini alarak uygulamayı oluşturabilirsiniz.
- Aşağıda Quadtree sınıfına ilişkin .h/.cpp dosyalarını bulabilirsiniz. Kod içerisindeki açıklamalar sizlere yardımcı olacaktır.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
//! Temel olarak kullanacagimiz quadtree sinifimiz //! Mevcut quadtree icerisindeki nesneler de sf::FloatRect'tir class BasicQuadtree { public: BasicQuadtree(int32_t level, const sf::FloatRect& boundary); //! Recursive olarak butun cocuklari temizler void Clear(); //! Bu metot ile mevcut quadtree node'u dorde bolunur ve her biri icin yeni sinirlar belirlenir void Split(); //! Verilen rectangle' icerisinde barindirabilecek olan cocuk dugumun indeksi. //! Eger herhangi bir cocuk dugume girmez ise -1 donulur ve ebeveyn dugum icerisine yerlestirilir int32_t GetIndex(const sf::FloatRect& rect); //! Eger eklendikten sonra bu dugum izin verilenden fazla nesne iceriyor ise bolumleme yapilir ve butun cocuklar dagitilir void Insert(const sf::FloatRect& rect); //! Verilen pRect ile kesisen butun nesneleri don void Retrieve(std::vector<sf::FloatRect>& returnedObjects, const sf::FloatRect& pRect); //! Verilen indeksi temsil eden cocuk dugum donulur BasicQuadtree* GetChildNode(int32_t index); //! Mevcut dugumun sinirlari donulur sf::FloatRect GetBoundary() const; //! Mevcut dugumun derinligi donulur uint32_t GetCurrentLevel() const; //! Bu dugumdeki nesneler donulur const std::vector<sf::FloatRect>& GetObjects(); protected: //! Bu dugumun bulundugu seviye. 0 en ust seviye anlamina gelir uint32_t mCurrentLevel = 0; //! Bu dugumde tutulan nesneler std::vector<sf::FloatRect> mObjects; //! Bu dugumun sinirlari sf::FloatRect mBoundary; //! Cocuk dugumler //! 0 => Sag ust, 1 => Sol ust, 2 => Sol alt, 3 => Sag alt std::unique_ptr<BasicQuadtree> mChildNodes[4]; }; |
İlgili quadtree sınıfının .cpp dosyasına da aşağıdan ulaşabilirsiniz.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 |
#include <BasicQuadtree.h> BasicQuadtree::BasicQuadtree(int32_t level, const sf::FloatRect& boundary) { mCurrentLevel = level; mBoundary = boundary; } void BasicQuadtree::Clear() { mObjects.clear(); for (auto& node : mChildNodes) { node = nullptr; } } void BasicQuadtree::Split() { float subWidth = mBoundary.width / 2.0F; float subHeight = mBoundary.height / 2.0F; float x = mBoundary.left; float y = mBoundary.top; // Cocuk dugumler icin yer alalim mChildNodes[0] = std::make_unique<BasicQuadtree>(mCurrentLevel + 1, sf::FloatRect(x + subWidth, y, subWidth, subHeight)); mChildNodes[1] = std::make_unique<BasicQuadtree>(mCurrentLevel + 1, sf::FloatRect(x, y, subWidth, subHeight)); mChildNodes[2] = std::make_unique<BasicQuadtree>(mCurrentLevel + 1, sf::FloatRect(x, y + subHeight, subWidth, subHeight)); mChildNodes[3] = std::make_unique<BasicQuadtree>(mCurrentLevel + 1, sf::FloatRect(x + subWidth, y + subHeight, subWidth, subHeight)); } int32_t BasicQuadtree::GetIndex(const sf::FloatRect& rect) { int32_t index = -1; float verticalMidpoint = mBoundary.left+ (mBoundary.width / 2); float horizontalMidpoint = mBoundary.top + (mBoundary.height / 2); // Verilen nesne ust bolumler icerisinde kaliyor mu bool topQuadrant = (rect.top < horizontalMidpoint) && ((rect.top + rect.height) < horizontalMidpoint); // Verilen nesne alt bolumler icerisinde kaliyor mu bool bottomQuadrant = (rect.top > horizontalMidpoint); // Verilen nesne sol bolumler icerisinde kaliyor mu if ((rect.left< verticalMidpoint) && (rect.left+ rect.width < verticalMidpoint)) { if (topQuadrant) { index = 1; } else if (bottomQuadrant) { index = 2; } } // Verilen nesne sag bolumler icerisinde kaliyor mu else if (rect.left> verticalMidpoint) { if (topQuadrant) { index = 0; } else if (bottomQuadrant) { index = 3; } } return index; } void BasicQuadtree::Insert(const sf::FloatRect& rect) { if (mChildNodes[0] != nullptr) { int32_t index = GetIndex(rect); // Bu dugum cocuk dugumlere sahip ve bu nesne onlardan ilgili olana eklenecek if (index != -1) { mChildNodes[index]->Insert(rect); return; } } // Eger bu nesnenin eklenebilecegi bir cocuk dugum yok ise bu dugume (ebeveyn) dugume ekleyelim mObjects.push_back(rect); // En alt seviyeye gelmedik fakat bu dugum icin nesne adeti doldu if ((mObjects.size() > gMaxObjectCount) && (mCurrentLevel < gMaxLevelCount)) { // Eger daha once bu dugum bolunmediyse dorde bolelim if (mChildNodes[0] == nullptr) { Split(); } size_t i = 0; while (i < mObjects.size()) { int32_t index = GetIndex(mObjects[i]); // Bu nesneyi cocuk dugume ekleyebiliriz if (index != -1) { // Once nesneyi yeni dugume ekleyelim mChildNodes[index]->Insert(mObjects[i]); // Daha sonra eski dugumden silelim mObjects.erase(mObjects.begin() + i); } // Bu nesneyi cocuk dugume ekleyemiyoruz else { i++; } } } } void BasicQuadtree::Retrieve(std::vector<sf::FloatRect>& returnedObjects, const sf::FloatRect& pRect) { int32_t index = GetIndex(pRect); if (index != -1 && mChildNodes[0] != nullptr) { mChildNodes[index]->Retrieve(returnedObjects, pRect); } returnedObjects.insert(returnedObjects.cend(), mObjects.cbegin(), mObjects.cend()); } BasicQuadtree* BasicQuadtree::GetChildNode(int32_t index) { BasicQuadtree* node = nullptr; if (index < 4) { node = mChildNodes[index].get(); } return node; } sf::FloatRect BasicQuadtree::GetBoundary() const { return mBoundary; } uint32_t BasicQuadtree::GetCurrentLevel() const { return mCurrentLevel; } const std::vector<sf::FloatRect>& BasicQuadtree::GetObjects() { return mObjects; } |
Bu sınıf ve örnek uygulama için https://github.com/yazilimperver/DataStructures ‘den ilgili kodları çekebilirsiniz. Örnek uygulama fare sol tıkı ile nesne eklemekte ve mevcut quadtree farklı renkler ile görselleştirilmekte. Daha önce de ifade ettiğim gibi bu çok basit ve performans vs göz önüne alınmadan yazılmış bir örnek. Sadece mantığı anlatmak adına bu şekilde yazıldı. Performans odaklı bir sürümünü de yakın zamanda ilgili “repository” ekleyeceğim canlar.
Sonuç
Sonuç olarak Quadtree’ler kolay bir veri yapısı olmaları sebebi ile 2B verilerin yönetilmesinde tercih edilebilirler. Alt düğüm sınırları çalışma zamanında hesaplanabilir. Düğümleri dinamik olarak çalışma zamanında bellekte oluşturmak yerine bir havuz yapısı kullanılması da performansı arttıracaktır. Noktasal veriler için kullanılacak Quadtree’ler ile alansal veya çizgisel nesneler için farklı ve özelleşmiş quadtree’ler kullanılabilir.
Her veri yapısında olduğu gibi ihtiyaçlarınız belirleyip ona göre Quadtree kullanımına karar vermelisiniz. Quadtree değilse peki ne sorusunun diğer muhatabı genelde “uniform grid” olur. Grid yapısı için de ayrıca bir yaz yazmayı planlıyorum.
Genel olarak dinamik nesnelerin ağırlıklı olduğu durumlarda uniform grid veya özelleşmiş quadtreeler tercih edilebilir. Ayrıca statik nesnelerin indekslenmesinde ise Quadtree’ler her ne kadar sorgulamada “uniform grid”‘e nazaran çok az bir şekilde yavaş olsa da boyut anlamında büyük avantaj sağlarlar. Bunun ile birlikte indeksleyeceğiniz nesnelerin boyutları değişkense bu da “uniform grid” için sıkıntı yaratabilir (hareket durumunda bir çok hücrede güncelleme gerekecektir).
Aşağıda Quadtree’lere ilişkin bir çok bağlantı bulabilirsiniz. Bir sonraki yazımda görüşmek üzere.
http://www.umiacs.umd.edu/~ramani/cmsc878R/p187-samet.pdf => Yine bu veri yapısı ile ilgili eski ama sağlam bir kaynak
http://jimkang.com/quadtreevis/ => İnteraktif bir quadtree uygulaması
https://web.archive.org/web/20120204170335/http://homepages.ge.ucl.ac.uk/~mhaklay/java.htm#PR => Quadtree, varyasyonları ve birçok diğer veri yapısı için başvurabilirsiniz.
https://github.com/timohausmann/quadtree-js => Javascript versiyonu
https://www.gamasutra.com/view/feature/3434/continuous_lod_terrain_meshing_.php?page=4 => Arazi görselleştirmesinde kullanımına bir örnek