SOLID 3 - Liskov'un Yerine Geçme Prensibi - Yazılımperver'in Dünyası

Umarım çoğunuz en son yazdığımız, QT soket uygulamasına bakabilmişsinizdir. Önümüzdeki dönem, bu kod üzerinde bir takım uygulamalar ve kabiliyetler daha geliştiriyor olacağız. Uzun süredir sizler ile birlikte olamadım, inşallah önümüzdeki dönemde, yazıların sıklığını biraz daha arttırmaya çalışacağım. Açıkçası bir süredir siteye SSL desteği kazandırma işine bakıyorum, bildiğiniz üzere bir süredir Google artık bu desteğe sahip olmayan siteleri direk chrome üzerinde güvensiz diye işaretliyor, ayrıca site görünürlüğünü de bunun etkilediğini ifade etmekte fayda var. Bu sebeple ilk fırsatta bu kabiliyeti ekleyeceğim. Bunun ile birlikte daha önce, sizler ile bazı videolar paylaşıyor ve bunlara ilişkin önemli noktalara dikkat çekmeye çalışıyordum, bu tip paylaşımları da önümüzdeki dönemde arttırıyor olacağım.

Şimdi gelelim bu yazımın konusuna. Bu yazımda SOLID prensiplerinin üçüncüsü olan “Liskov Substitution Principle“‘a, kısaca LSP’ye, bakacağız. Aşağıdaki uzaylı arkadaşların da ifade ettiği üzere bu prensipler oldukça önemli :), bundan sonra hızlıca diğer prensipleri de bitirmeyi planlıyorum.

Öncelikle, sizlerin de akıllarında bir soru işareti olan bu prensibin isminin nereden geldiğine bir göz atalım. Bu prensip ilk olarak Barbar Liskov adında bir kadın tarafından veri soyutlama ve tip teorisi çalışmalarında ifade edilmiş, kendisi de bu kavramı Bertrand Meyer’in “Design by Contract” çalışmasından türetmiştir. Bu çalışmalara ilişkin detaylı bilgilere kaynaklar kısmından ulaşabilirsiniz. Bu yazımda da yine, Bob amcanın ifadelerine bolca atıfta bulunacağım.

Diğer SOLID yazılarına aşağıdaki bağlantılardan ulaşabilirsiniz. Aynı zamanda SOLID prensipler genel anlamda neye hizmet ediyor ve genel motivasyon için de ilk yazıya başvurabilirsiniz:

SOLID 1 – Tek Sorumluluk Prensibi
SOLID 2 – Açık/Kapalı Prensibi
SOLID 3 – “Liskov Substitution” Prensibi
SOLID 4 – Arayüz Ayrıştırma Prensibi

Liskov‘un Yerine Geçme Prensibi

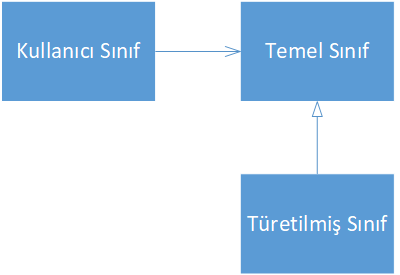
Peki bu prensip bizlere ne söyler? Orijinal ifadesi ile “Subclasses should be substitutable for their base classes“, her bir alt sınıf, türetilmiş olduğu, temel sınıflar yerine kullanılabiliyor olmalıdır. Bir diğer ifade ile, temel sınıfı kullanan herhangi bir kullanıcı sınıf, aynı şekilde, bu temel sınıftan türetilmiş olan sınıfı da kullanabiliyor olmalıdır. Bunu aşağıdaki figür ile gösterebiliriz.

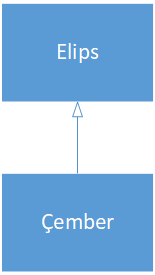
Bu ifade, ilk bakışta, gayet açık gelebilir, ama burada göz önünde bulundurmamız gereken bir takım hususlar var. Buna geometrik sınıflar üzerinden bir göz atalım. Bu anlamda Çember/Elipse sınıflarına ve bunların ilişkilerini ele alalım. Çoğumuz bu iki sınıfı düşünürken, aslında elipsin daha genel ve çemberin de aslında elipsin özel bir durumu olduğunu düşüne gelmişizdir. Bu da bizi, bu iki sınıfı miras mekanizması ile ilişkilendirmeye itebilir. Bunun sonucu olarak, elips temel sınıf ve çember de bunun alt sınıfı olarak kabul edilebilir.

İlk bakışta bu yaklaşımda herhangi bir sıkıntı görünmese de, biraz daha yakından baktığımızda bir takım hususların kendisini göstereceğini göreceğiz. Bunun öncesinde bu sınıfları koda dökelim. Öncelikle elips ile başlayalım.

Burada temel olarak elips, aslında iki farklı yarı çap ile ifade ediliyor ve örneğimiz için şimdilik sadece alan hesapladığımızı düşünelim.

// Bizim elips temel sinifimiz
class Ellipse
{
public:
    virtual void setRadiusA(double a) {
        mRadiusA = a;
    }
    virtual void setRadiusB(double b) {
        mRadiusB = b;
    }

    virtual double calculateArea() {
        return mRadiusA * mRadiusB * PI;
    }
protected:
    double mRadiusA;
    double mRadiusB;
};

// Bizim elips temel sinifimiz

class Ellipse

{

public:

virtual void setRadiusA(double a) {

mRadiusA = a;

}

virtual void setRadiusB(double b) {

mRadiusB = b;

}

virtual double calculateArea() {

return mRadiusA * mRadiusB * PI;

}

protected:

double mRadiusA;

double mRadiusB;

};

Şimdi gelelim çember sınıfımıza. Çember sınıfımız elipsten farklı olarak, tek bir yarıçapa ihtiyaç duyuyor. Bunu nasıl çözeriz? Bu amaçla, yarıçap metotlarından birini bu amaç ile kullanabiliriz.

// Cember sinifimiz
class Circle
  : public Ellipse
{
public:
    virtual void setRadiusA(double a) override {
        Ellipse::setRadiusA(a);
        mRadiusB = a;
    }
};

// Cember sinifimiz

class Circle

: public Ellipse

{

public:

virtual void setRadiusA(double a) override {

Ellipse::setRadiusA(a);

mRadiusB = a;

}

};

Evet, bu sınıf ile ne gibi bir problem yaşayabiliriz sizce? Bir kullanıcı sınıfımız bir şekilde setRadiusB metodunu farklı bir değer ile çağırır ise çembere ilişkin alan metodumuz bizlere yanlış sonuç verecektir:

...
auto circle = std::make_unique<Circle>();
circle.setRadiusA(5);
circle.setRadiusB(4);

// Cikit: 5*4*PI = 62.83, ama bekledigimiz deger 5*5*PI = 78.54
std::cout << "Area is: " << circle->calculateArea(); 

...

...

auto circle = std::make_unique<Circle>();

circle.setRadiusA(5);

circle.setRadiusB(4);

// Cikit: 5*4*PI = 62.83, ama bekledigimiz deger 5*5*PI = 78.54

std::cout << "Area is: " << circle->calculateArea();

...

Bu problemi, bu yaklaşımla bir kaç farklı yol ile çözebiliriz. İlk yöntem çember için setRadius gibi bir metot ekleyebilir ve alan hesaplamasını bunun üzerinden yapabiliriz:

// Cember sinifimiz
class Circle
  : public Ellipse
{
public:
    void setRadius(double r){
        mRadius = r;
    }

   virtual double calculateArea() override
   {
      return mRadius * mRadius * PI;
   }
protected:
    double mRadius;
};

// Cember sinifimiz

class Circle

: public Ellipse

{

public:

void setRadius(double r){

mRadius = r;

}

virtual double calculateArea() override

{

return mRadius * mRadius * PI;

}

protected:

double mRadius;

};

Ya da elips sınıfında bulunan her iki metodu da bu bağlamda güncelleyebiliriz:

// Cember sinifimiz
class Circle
  : public Ellipse
{
public:
    virtual void setRadiusA(double a) override {
        Ellipse::setRadiusA(a);
        mRadiusB = a;
    }
    virtual void setRadiusB(double a) override {
        Ellipse::setRadiusB(a);
        mRadiusA = a;
    }
};

// Cember sinifimiz

class Circle

: public Ellipse

{

public:

virtual void setRadiusA(double a) override {

Ellipse::setRadiusA(a);

mRadiusB = a;

}

virtual void setRadiusB(double a) override {

Ellipse::setRadiusB(a);

mRadiusA = a;

}

};

Şimdi her iki çözüm yöntemi de kendine has sıkıntıları barındırıyor. Bir kere eminim hepiniz bu iki çözümün de derme çatma olduğunu kabul edecektir ve alan hesaplama dışında benzer ihtiyaçlarda, bu sıkıntı katlanarak devam edecektir. Bir diğer sıkıntı da, aslında temelde yaklaşımımızdaki hata, yani çember aslında elipsten farklı (türetilmiş de olsa) bir sınıf değil, aslında onun özel bir şekilde ifade ediliş hali, yani bu şekilde modellemek pek doğru değil. Sonuç olarak, çember diye ayrı bir sınıf oluşturmaktan sa, elips sınıfını mevcut hali ile her iki durum için de kullanmak daha doğru bir yaklaşım olacaktır. Zaten bir çok görselleştirme kütüphanesine bakacak olursanız, genelde çember çizdirme API’si yerine sadece elips çizim API’si sunulur (ör. QT QPainter sınıfı).

LSP’ye ilişkin ihlallerin bulunması, bazen gerçekten zor olabilmektedir. Bazı durumlarda aslında, OCP’nin de ihlal edildiği görülebilecektir. Sonuç olarak türetilmiş sınıf nesneleri, temel sınıfın davranışlarını değiştirmemeli/yerine geçmemeli, tamamlayıcı ek davranışlar sunmalı.

Şimdi gelelim ördek meselesine 🙂 Bu aslında ördek testi denilen bir test ile de ifade edilebilir. Şöyle ki: “Eğer bir şey ördek gibi görünüyor, onun gibi yüzüyor, onun gibi de vakvaklıyor ise, muhtemelen o bir ördektir.”. Bunu LSP’ye çevirecek olursak, “Eğer bir şey ördek gibi görünüyor, onun gibi yüzüyor, ama pile ihtiyaç duyuyor ise, muhtemelen yanlış bir soyutlamaya sahipsiniz :).”

Paylaşmak güzeldir.

SOLID 3 – Liskov’un Yerine Geçme Prensibi

Liskov‘un Yerine Geçme Prensibi

Kaynaklar:

Bir cevap yazın Cevabı iptal et